Injective object

In mathematics, especially in the field of category theory, the concept of injective object is a generalization of the concept of injective module. This concept is important in homotopy theory and in theory of model categories. The dual notion is that of a projective object.

1 General Definition
2 Abelian case
3 Enough injectives
4 Injective hull
5 Examples
6 References

General Definition

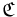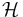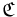Let $\mathfrak{C}$ be a category and let $\mathcal{H}$ be a class of morphisms of $\mathfrak{C}$ .

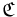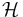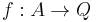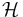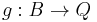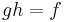An object $Q$ of $\mathfrak{C}$ is said to be $\mathcal{H}$ -injective if for every arrow $f: A \to Q$ and every morphism $h: A \to B$ in $\mathcal{H}$ there exists a morphism $g: B \to Q$ extending (the domain of) $f$ , i.e $gh = f$ . In other words, $Q$ is injective iff any 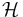$\mathcal{H}$ -morphism extends (via composition on the left) to any morphism into $Q$ .

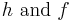The morphism $g$ in the above definition is not required to be uniquely determined by $h \text{ and } f$ .

In a locally small category, it is equivalent to require that the hom functor 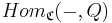$Hom_{\mathfrak{C}}(-,Q)$ carries 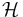$\mathcal{H}$ -morphisms to epimorphisms (surjections).

The classical choice for 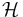$\mathcal{H}$ is the class of monomorphisms, in this case, the expression injective object is used.

Abelian case

If 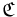$\mathfrak{C}$ is an abelian category, an object A of 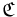$\mathfrak{C}$ is injective iff its hom functor Hom_C(–,A) is exact.

The abelian case was the original framework for the notion of injectivity.

Enough injectives

Let 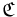$\mathfrak{C}$ be a category, H a class of morphisms of 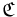$\mathfrak{C}$ ; the category 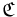$\mathfrak{C}$ is said to have enough H-injectives if for every object X of 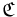$\mathfrak{C}$ , there exist a H-morphism from X to an H-injective object.

Injective hull

A H-morphism g in 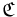$\mathfrak{C}$ is called H-essential if for any morphism f, the composite fg is in H only if f is in H.

If f is a H-essential H-morphism with a domain X and an H-injective codomain G, G is called an H-injective hull of X. This H-injective hull is then unique up to a canonical isomorphism.

Examples

In the category of Abelian groups and group homomorphisms, an injective object is a divisible group.
In the category of modules and module homomorphisms, R-Mod, an injective object is an injective module. R-Mod has injective hulls (as a consequence, R-Mod has enough injectives).
In the category of metric spaces and nonexpansive mappings, Met, an injective object is an injective metric space, and the injective hull of a metric space is its tight span.
In the category of T0 spaces and continuous mappings, an injective object is always a Scott topology on a continuous lattice therefore it is always sober and locally compact.
In the category of simplicial sets, the injective objects with respect to the class of anodyne extensions are Kan complexes.
In the category of partially ordered sets and monotonic functions between posets, the complete lattices form the injective objects for order-embeddings, and the Dedekind–MacNeille completion of a partially ordered set is its injective hull.
One also talks about injective objects in more general categories, for instance in functor categories or in categories of sheaves of O_X modules over some ringed space (X,O_X).

References

J. Rosicky, Injectivity and accessible categories
F. Cagliari and S. Montovani, T₀-reflection and injective hulls of fibre spaces